많은 머싱 러닝 알고리즘은 입력 데이터가 선형적으로 구분 가능하다는 가정을 한다.

선형적으로 완벽하게 분리하지 못하는 이유는 잡음 때문이라고 가정한다.
만일 비선형 문제를 다루어야 한다면 PCA, LDA 같은 차원 축소를 위한 선형 기법은 최선의 선택이 아니다.
이 때 커널 PCA(KPCA)를 이용한다.
커널 PCA를 이용하여 선형적으로 구분되지 않는 데이터를 선형 분류기에 적합한 새로운 저차원
부분 공간으로 변환하는 방법이다.

Kernel PCA(커널 PCA)
비선형 매핑을 수행하여 데이터를 고차원 공간으로 변환한다.
그 다음 고차원 공간에 표준 PCA를 사용하여 샘플이 선형 분류기로 구분될 수 있는 저차원 공간으로
데이터를 투영한다.(샘플이 이 입력 공간에서 잘 구분된다고 가정)
단 위 방법은 계산 비용이 매우 비싸다.
Kernel Trick(커널 트릭)
커널 트릭을 이용하면, 원본 특성 공간에서 두 고차원 특성 벡터의 유사도를 계산할 수 있다.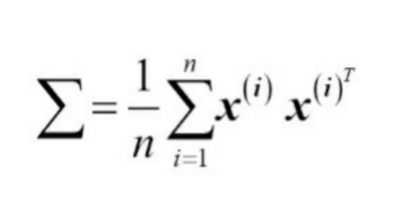
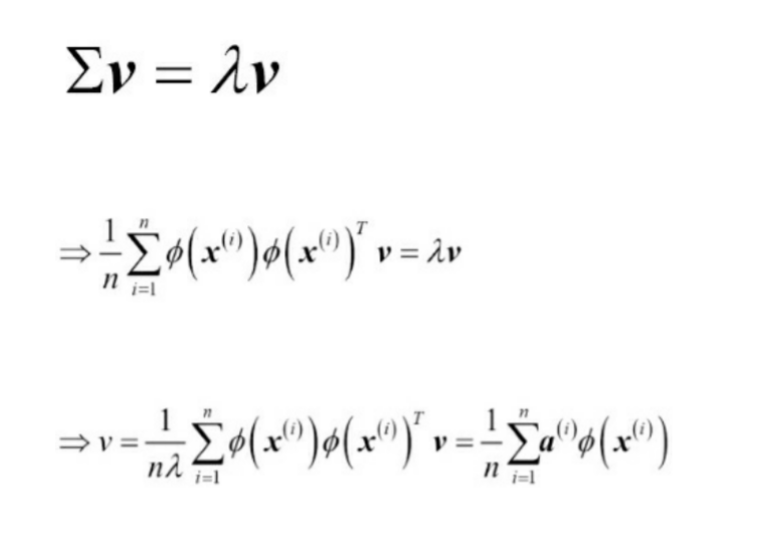

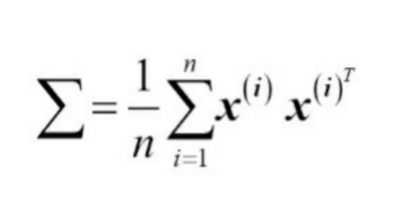
베른하르트 슐코프(Bernhard Scholkopf)는 위 방식을 일반화하여, 비선형 특성 조합으로
원본 특성 공간의 샘플 사이의 점곱을 대체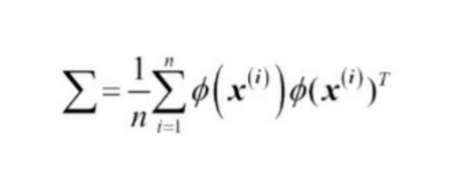
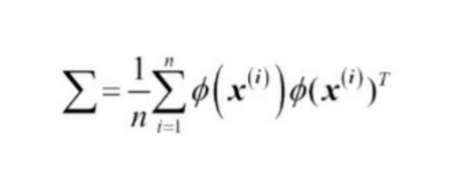
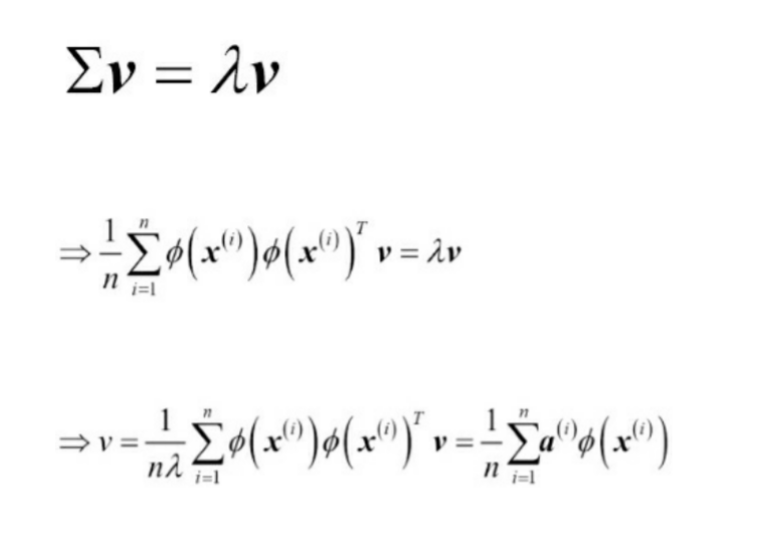
식을 위와 같이 변형할 수 있다.

K는 유사도(커널) 행렬이다. K의 고유 벡터를 추출함으로써 a값을 구할 수 있다.
머싱러닝교과서with파이썬, 사이킷런, 텐서플로_개정3판 pg.220
커널 트릭을 이용하여 샘플 x끼리의 pi함수 점곱을 커널 함수 K로 바꾸면
고유 벡터를 명시적으로 계산할 필요가 없다.
커널 PCA를 통해서 얻은 것은 표준 PCA 방식에서 투영 행렬을 구성한 것이 아니고
각각의 성분에 이미 투영된 샘플이다.
기본적으로 커널 함수(kernel)은 두 벡터 사이의 점곱을 계산할 수 있는 함수, 유사도를 측정할 수 있는 함수이다.
(kernel SVM과 동일하게 적용)
많이 사용 되는 커널
다항커널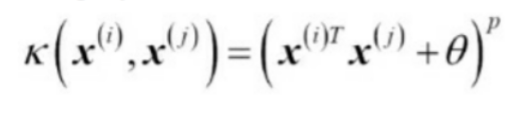
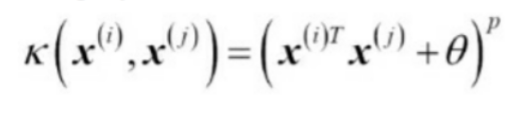
하이퍼볼릭 탄젠트(hyperbolic tangent)(시그모이드(sigmoid)) 커널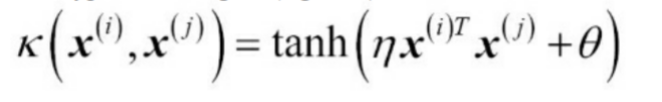
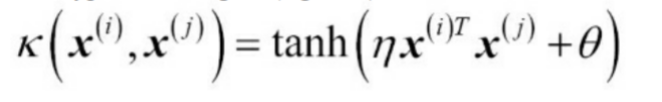
방사기저항수(Radial Basis Function, RBF), 가우시안 커
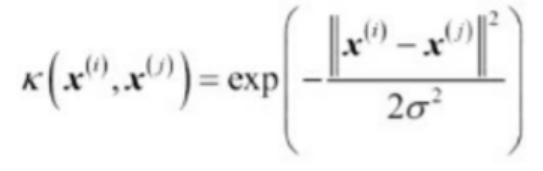
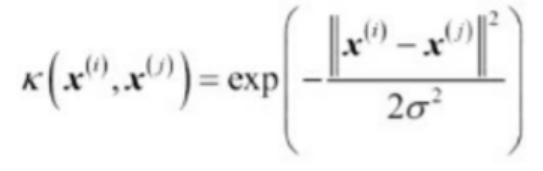
process of KPCA
1. 커널(유사도) 행렬 K를 계산

ex) 100개의 훈련 샘플이 담긴 데이터셋은 각 쌍의 유사도를 담은 대칭 커널 행렬 100X100 차원이 된다.

2. 다음 식을 사용하여 커널 행렬 K를 중앙에 맞춘다.
1(n)은 모든 값이 1/n인 nXn차원 행렬

3. 고윳값 크기대로 내림차순으로 정렬하여 중앙에 맞춘 커널 행렬에서 최상위 k개의 고유 벡터를 고른다.
KernelCenter클래스
scikitlearn KernelCenter클래스를 이용해서 커널을 중앙에 맞출수 있다.
from sklearn.preprocessing import KernelCenterer
K_centered=KernelCenterer().fit_transform(K)